信息网络安全 | 笔记二
第4章 单（私）钥密码体制
4.1 密码体制的定义
密码体制的语法定义：
- 明文消息空间：
- 密文消息空间：
- 加密密钥空间：
- 解密密钥空间：
- 有效的密钥生成算法
- 加密算法
- 解密算法
- 密钥生成算法
- 加密/解密过程
密码体制的分类：
若加密密钥=解密密钥，则为单钥加密体制（对称加密体制、私钥密码体制）
单钥密码分为：
- 流密码（序列密码）
- 分组密码
若加密密钥≠解密密钥，则为双钥密码体制（非对称加密、公钥密码体制）
Kerckhoffs原理：一个密码系统的安全性不应取决于其设计或实施的保密性。相反，系统的安全性应该完全取决于钥匙的保密性。
4.2 古典密码
古典密码的两大基本方法：
- 置换密码：明文字母保持不变，但顺序被打乱
- 代换密码：明文字母被替换，但顺序不变
代换密码包括：
单表代换：凯撒密码
多表代换：维吉尼亚密码
弗纳姆密码：消息与密钥逐比特异或。
如果密钥串只使用一次，那么是一次一密密码。
弗纳姆密码可以看成流密码的雏形。
置换密码：可以使用矩阵，每次置换都可以表示为与一个置换矩阵的乘积，并且有一个与之对应的逆置换矩阵。
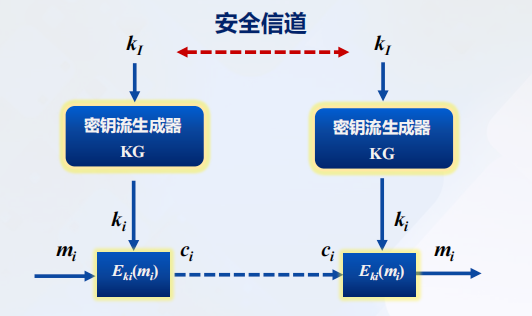
4.3 流密码的基本概念
流密码特点：
- 解密过程和加密过程相同且互逆
- 流密码的安全性完全依赖于伪随机数的强度
4.4 快速软、硬件实现的流密码算法
第5章 双（公）钥密码体制
5.1 双钥密码体制的基本概念
单向函数：
对一个可逆函数
陷门单向函数：
单向函数是求逆困难的函数，而陷门单向函数是在不知道陷门信息下求逆困难的函数。当知道陷门信息后，求逆易于实现。
用于构造双钥密码的单向函数：
- 多项式求根
- 离散对数(discrete logarithms problem, DL)
- 大整数分解FAC
- Diffie-Hellman问题(DHP)
- 背包问题
- 二次剩余问题
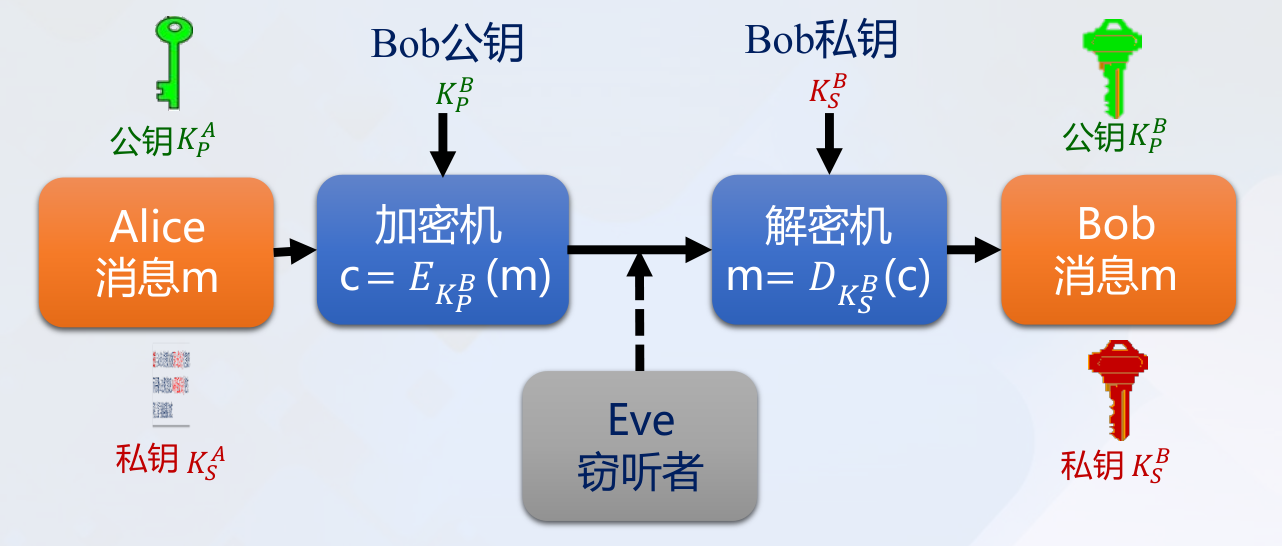
公钥密码的特点：
- 每个用户都拥有两个密钥：公钥和私钥
- 公钥密码解决了密钥发布和管理问题
公钥密码的用途：
- 密钥分发
- 消息加密
- 数字签名
公钥密码的安全性：
- 安全性依赖于数学的困难问题
- 穷搜索在理论上能破解公钥密码，但是在密钥足够长时破解极其困难
- 加密速度慢，一般用于密钥传递而不用于实时的数据加密
5.2 RSA密码体制
RSA安全性基于大整数分解的困难性
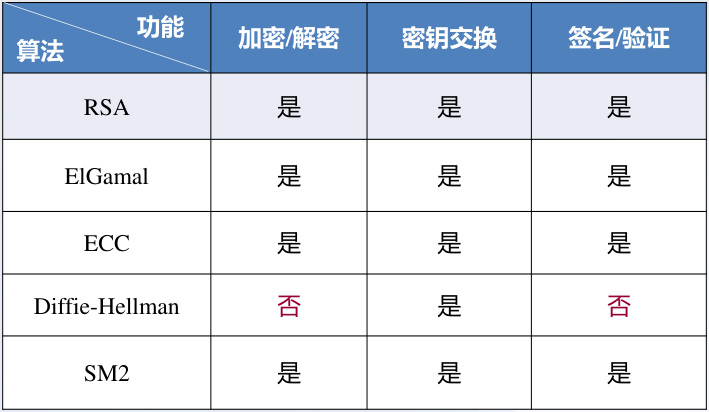
可以用于：消息加密、数字签名
RSA算法说明
因此有：
加密：
RSA密钥选择
- 模数大于1024bit，p, q为大素数
- p-1，q-1有大的素因子
- p+1，q+1也要有大的素因子
- e不能太小，例如 e 值为3，17，65537，（2^16+1）
RSA算法的特点
- 只要A知道B的公钥，就可以进行保密通信
- 速度慢，不适合对语音等进行实时加密
- 要求对公钥进行保护，防止公钥被修改和替换
RSA算法的安全性
MIPS年：Million Instructions Per Second 用每秒完成100万条指令的计算机所需工作的年数
RSA的安全性取决于模n分解的困难性
5.3 ElGamal密码体制
ElGamal公钥密码安全性依赖于离散对数问题
密钥生成算法：
- 选取一个足够大的素数
，在 上选取一个本原元 - 随机选取一个整数
，并计算 - 公钥为
，私钥为
加密：
消息
。 选择任意整数
得到密文对：
解密：
5.4 Diffie-Hellman公钥密码体制
算法过程：
- AB协商一个大素数p和本原根a，a和p公开
- A产生随机数x，计算
，X发给B - B产生随机数y，计算
，Y发给A - A计算
- B计算
D-H协议的安全性：不能抵抗中间人攻击
D-H协议应用：空间网络密钥的自动分发和更新
5.5 椭圆曲线密码体制（ECC）
定义：
根据群的定义可知，
可以采用 Montgomery 阶梯算法，并行、高效计算
椭圆曲线的安全性
椭圆曲线密码体制的安全性基于：椭圆曲线上的离散对数问题 ECDLP
在
椭圆曲线上的公钥算法
- 椭圆曲线的DH密钥交换算法
- 椭圆曲线的ElGamal密码体制
优势
最大的优势在于可以使用比RSA更短的密钥来获得相同水平的安全性，从而使计算量大大减少
应用
- 无线MODEM
- Web服务器：ECC可以节省计算的时间和带宽，并且通过算法的协商更易于处理兼容性问题。
- 集成电路卡：ECC无需协处理器就可以在IC卡上实现快速安全的数字签名，大大降低了IC卡的成本
5.6 中国商用密码SM2算法
特点：
- 基于椭圆曲线，使用256位素数域
上的椭圆曲线 - 包含加解密算法、数字签名算法、密钥交换协议
- 采取了检错措施，提高了系统的数据完整性和可靠性
5.7 其它公钥密码
第6章 消息认证和杂凑函数
6.1 消息的真实性与认证
- 对称认证：双方互相信任的认证 主要防止来自第三方的攻击，例如文件是否被人修改过
- 非对称认证：双方互相不信任的认证 主要防止来自对方的攻击，例如收到的文件是否真实
6.2 杂凑（Hash）函数
杂凑函数是将任意长的数字串M映射成一个较短的定长输出数字串H的函数。
常用hash函数：
- MD5
- SHA
- 采用分组密码算法构造的hash函数
单向杂凑函数
- 快速性：任给x，计算
容易 - 单向性：任给y，由
计算x困难 - 无碰撞：寻找
，满足 是苦难的
单向杂凑函数的特点：
- 算法特点：不定长的输入，固定长度的输出
- 雪崩效应：输入发生很小的改动，则可引发输出较大的变动
- 完全单向：已知输出无法推算出输入，已知两个输出的差别无法推算出输入的差别
抗碰撞杂凑函数（CRHF）
- 强单向杂凑函数 对任意给定的
，要找到 ，使得两则杂凑值相等，在计算上是不可行的 - 弱单向杂凑函数 若要找到任意一对输入
、 ，两者不相等并且杂凑值相等，在计算上是不可行的
杂凑函数的安全性
- 抗碰撞攻击 找到两个不同的消息
，使得 在计算上不可行 - 抗原象攻击 给定任意n-bit的杂凑值
，找到一个 ，使得 在计算上不可行 - 抗第二原象攻击 给定任意消息
，找到另一个消息 ，使得 在计算上不可行
6.3 消息认证码与消息检测码
消息认证码（MAC: Message Authentication Code） MAC算法是有密钥参与杂凑运算的算法
，其中 是收发双方共享的密钥 消息检测码（MDC: Message Detection Code） MDC算法是无密钥参与杂凑运算的算法
若消息很长，MDC可以用迭代方法构造：
- 消息X被分为t个分组，如必要，则需填充补位（padding）
H为哈希函数，f为轮函数，g为输出变换 IV和padding的方式对安全性有重大影响
6.4 杂凑函数的应用
杂凑函数的应用：
- 数字签名 先对消息杂凑得到MDC，对MDC进行数字签名，验证时只需验证MDC的正确性
- 消息篡改检测 用于验证消息的完整性验证
- 随机数发生器
构造MAC：
- 消息真实性依赖于共享密钥k的真实性和保密性
- 任意拥有此密钥的人均可以验证消息的真实性
- 对消息真实性的保护转化成安全地在通信双方之间建立共享密钥的问题
构造MDC：
应为抗碰撞的杂凑函数
6.5 应用杂凑函数的基本方式
- 既提供保密性，又提供消息认证
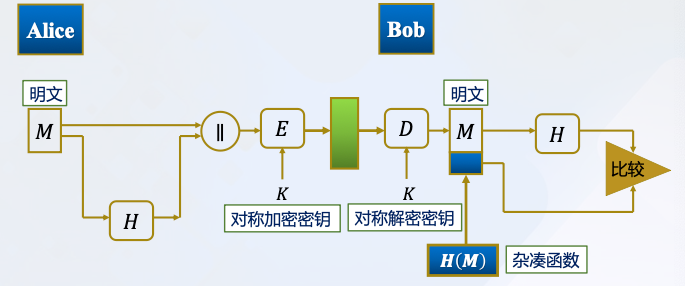
提供保密性：只有Alice和Bob共享密钥 𝐾
提供认证：𝐻(𝑀) 受密码保护
- 仅仅提供消息认证
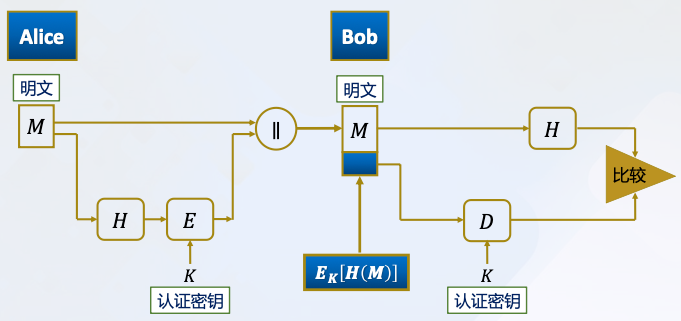
提供认证：𝐻(𝑀) 受密码保护
- 既提供消息认证，又提供数字签名
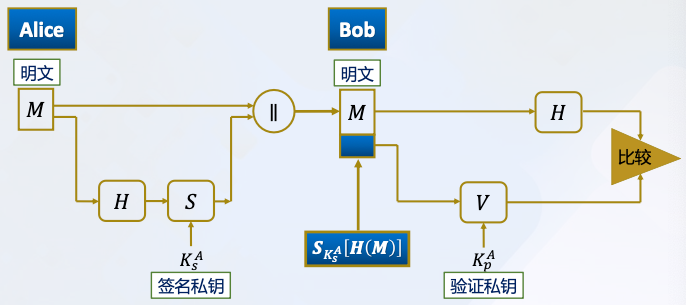
提供数字签名：只有Alice能产生
提供认证：
- 既提供保密性，又提供消息认证和数字签名
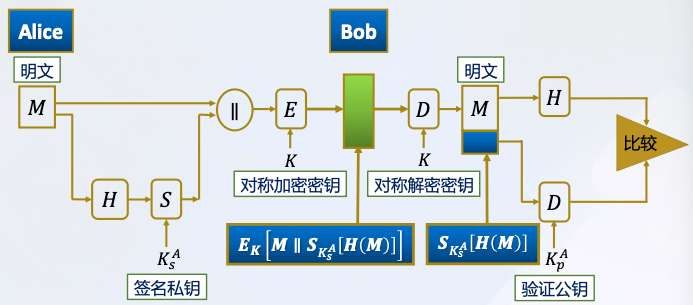
提供保密性：只有Alice和Bob共享密钥 𝐾
提供数字签名：只有Alice能产生
提供认证：
- 仅提供消息认证
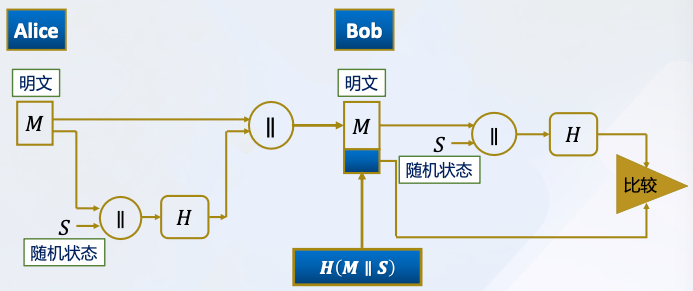
提供认证：只有Alice和Bob共享随机状态𝑆
- 既提供保密性，又提供消息认证
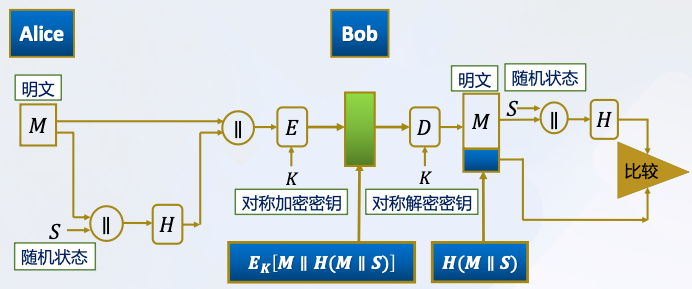
提供保密性：只有Alice和Bob共享密钥𝐾
提供认证：只有Alice和Bob共享随机状态𝑆
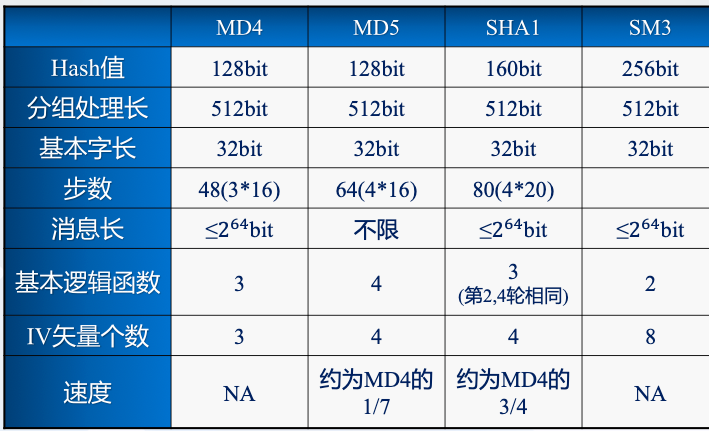
6.6 常用杂凑函数
2010年，国家密码管理局颁布了中国商用密码杂凑函数SM3。
SM3是一种采用Merkle-Damgard结构的杂凑函数。
第7章 数字签名
7.1 数字签名的基本概念
数字签名应满足的条件：
- R1条件：收方能够确认或证实发方的签名，但不能伪造签名
- S条件：发方发出签名的消息给收方后，不能再否认他所签发的消息
- R2条件：收方对已收到的签名消息不能否认，即有收报认证
- T条件：第三者可以确认收发双方之间的消息传送，但不能伪造这一过程
签名体制的安全性：
- 给定消息
和签名 ，难以推出签名者的私钥sk - 很难伪造另外一个消息
，是得
7.2 RSA签名体制
安全性依赖于大整数分解困难问题
7.3 ElGamal签名体制
当重复使用同一个
要确保此签名体制的安全性，就必须保证每次签名时，选择不同的随机数
7.4 Schnorr签名体制
Schnorr的签名长度要比ElGamal短，安全性也比ElGamal差
7.5 DSS签名体制
美国联邦信息处理标准，该体制基于ElGamal和Schnorr签名体制设计
7.6 中国商用签名体制SM2
基于椭圆曲线的公钥密码算法
7.7 具有特殊功能的数字签名体制
不可否认签名（Undeniable Signature）
这类签名要求在签名者合作下才能验证签名
防失败签名（Fail-Stop Signature）
盲签名（Blind Signature）
群签名（Group Signature）
代理签名（Proxy Signature）
指定证实人签名（Designated Confirmer Signature）
一次性签名（One-Time Signature）
7.8 数字签名的应用
第8章 密码协议
8.1 协议的基本概念
协议是指由两个或两个以上的参与者为完成某项特定的任务而采取的一系列步骤。
协议的特点：
- 协议自始至终是有序的过程，每一步骤必须依次执行。
- 协议至少需要两个参与者。
- 通过执行协议必须能够完成某项任务。
密码协议，也称安全协议。它由多方参与执行，并达到秘密信息交换、实体身份认证和信息完整性保护的安全目标。一般而言，密码学中所有的密码系统，例如密钥分配系统、身份认证系统、秘密共享系统，均使用了密码协议。
1. 仲裁协议
Trent为仲裁者(Arbitrator)，是公正的第三方，各方均信赖他。
- “公正”意味着仲裁者对参与协议的任何一方没有偏向
- “可信赖”意味着双方相信他所说的话、做的事
- 仲裁者将帮助两个互不信赖的实体完成协议
仲裁协议的问题：
- 在互不信任的通信双方进行通信时，仲裁者也可能被怀疑
- 需要额外的费用开销
- 增加处理时延，可能成为系统的瓶颈
- 仲裁者可能会成为黑客的攻击目标
2. 裁决协议
裁决人(Adjudicator)也是公正的、可信赖的第三方Trent，但他不直接参与协议。这是区别于仲裁协议的情况。
一旦通信双方发生纠纷，则需要双方向裁决人提供各自掌握的证据，由裁决人来加以裁决。无纠纷时裁决人不参与通信。
- 裁决协议建立在通信双方均是诚实的基础上。
- 当有人怀疑发生欺骗时，可信赖的第三方就可以根据所提供的证据判定是否存在欺骗。
- 一个好的裁决协议应当能够确定欺骗者的身份。
- 裁决协议只检测欺骗是否存在，但不能防止欺骗的发生。
3. 自动执行协议
自执行协议(self-enforcing)是最好的协议，协议本身就保证了公平性。
这种协议不需要仲裁者的参与，也不需要仲裁者解决争端。
如果协议中的一方试图欺骗另一方，那么另一方会立刻检测到该欺骗的发生，并停止执行协议。
好的协议应具备的特点：
- 协议涉及的各方必须事先知道此协议的所有步骤
- 协议涉及的各方必须同意、遵守协议
- 协议必须是非模糊的。对协议的每一步都必须确切定义，力求避免产生误解
- 协议必须是完整的
- 每一步操作要么是由一方或多方进行计算，要么是在各方之间进行消息传递，二者必居其一
8.2 安全协议分类及基本密码协议
安全协议的分类：
- 认证协议 (authentication protocol)：向一个实体提供关于另外一个实体身份的确信度
- 密钥建立协议 (key establishment protocol)： 在两个通信实体之间建立共享密钥
- 认证的密钥建立协议(authenticated key establishment protocol)：在另一实体的身份已被证实的基础之上两个通信实体之间建立共享密钥。
1. 密钥建立协议
密钥建立协议目标：可在通信实体之间建立会话密钥
采用单钥体制的密钥建立协议
采用双钥体制的密钥建立协议
不能抵抗中间人攻击，需要采用PKI/CA数字证书技术
中间人攻击
联锁协议
联锁协议可以有效地抵抗中间人攻击
在具体实现中：
- 有初始向量IV的分组加密中，前半个消息：密文，后半个消息：初始向量
- 在带有杂凑函数的算法中，前半个消息：加密消息的杂凑值，后半个消息：密文
采用数字签名的密钥交换
单双钥混合实现密钥和消息传输
密钥和消息广播
Diffie-Hellman密钥交换协议
Diffie-Hellman攻击不能抵抗中间人攻击
2. 认证协议
认证包含消息认证、数据源认证和实体认证
传统上采用口令认证的方式比较脆弱，需要设计安全的认证协议
分为单向认证和双向认证
采用单向函数的认证协议
采用双钥体制的认证
认证是单向的
采用联锁协议的双向认证
可以对此协议成功实施中间人攻击
单向SKID身份识别协议—SKID2
双向SKID身份识别协议—SKID3
消息认证
3. 认证的密钥建立协议
这类协议将认证和密钥建立结合在一起，使Alice和Bob确信他正在与可信赖的另一方进行保密通信。
密钥认证分为三种：
- 隐式密钥认证：识别Bob的身份
- 密钥确认：确认Bob拥有的密钥值
- 显式密钥确认：隐式密钥认证 + 密钥确证
常用的协议方法：
- 大嘴青蛙协议（单钥）
- Yahalom协议（单钥）
- Kerberos协议（单钥）
- EKE协议（单钥+双钥）
8.3 秘密分拆协议
2方的秘密拆分协议：
随机生成一个与消息同长的比特串R，与消息M异或得到S，并将R与S分发，只有两者异或时才可以恢复出M。
4方的秘密拆分协议：
随机生成三个比特串
8.4 密码协议的安全性
安全性验证方法：
- 攻击检验法
- 形式语言逻辑分析法
- 可证安全性分析
常用的攻击方法：
- 已知明文攻击
- 选择密文攻击
- 预言者会话攻击
- 并行会话攻击
常用的形式化语言逻辑：
- BAN
- GNY
- 此外，还有AT逻辑、VO逻辑、SVO逻辑等。SVO=BAN+GNY+AT+SO