秘密共享

1. 基本概念

1.1 介绍

参考资料：《密码协议基础》第8章

1.2 符号介绍

：全部参与的人数

：门限值，即任意t个参与者可以恢复出秘密，但少于t个参与者无法计算出关于原秘密的任何信息

是q阶有限域，其中

为素数

：要分享的秘密

：秘密碎片

：秘密分发者

：参与者

2. Shamir 秘密分享体制

2.1 前置知识：Lagrange插值多项式

已知n+1个点x1，x2，…，xn的函数值，可以使用lagrange插值求出一个n次多项式插值函数f(x),f(x)是接近未知原函数p(x)的函数，根据插值函数f(x)求出p(x)的未知点.

拉格朗日插值基函数：

拉格朗日插值多项式公式：

2.2 秘密分发

1. D随机选择一个t阶多项式 ，并且
2. D将 发送给

2.3 秘密重构

利用Lagrange插值多项式可以计算出： 其中，

由于秘密是，则令，得到：

1. 共t个参与者，参与者每个人计算：
2. 恢复得到秘密：

3. 可验证秘密共享VSS

3.1 介绍

为解决不诚实分发中心的问题，秘密分发者不仅分发秘密的碎片，而且广播对秘密碎片的承诺，各成员收到碎片时，验证碎片是否正确，重构阶段也验证其他成员的秘密碎片的正确性。

因此相对于Shamir只能抵抗被动攻击，VSS可以抵抗分发者分发错误碎片和参与者提交错误碎片的主动攻击。

3.2 Feldman的VSS方案

为一个 大素数， 为 阶循环群， 为生成元

3.2.1 秘密分发

1. D选择一个随机多项式：，其中 ，各项系数均属于 。

2. D将 发送给

3. D广播承诺

4. 参与者 收到自己的碎片 后，计算下式是否成立： 如果成立，表明该碎片有效；若不成立，则请求D重发正确的碎片

3.2.2 秘密重构

重构方法同Shamir 秘密分享体制，任意t个参与者向参与重构的其他合作者秘密广播自己的碎片，这样每个参与重构的成员都可以通过上述的方法验证所收到的碎片的有效性，并利用拉格朗日插值定理重构出秘密s。

3.3 Pedersen的VSS方案

Feldman的方案中将 也作为一个承诺发出，只是计算安全的。Petersen方案中进行了进一步的扩展，不会直接泄露秘密s，是无条件安全的。

为一个 大素数， 为 阶循环群， 为生成元， 是一个随机元素

3.3.1 秘密分发

1. D选取两个随机多项式$a(x) = {j = 0}^{t-1}a_txt ,b(x) = {j = 0}^{t-1}b_txt a_0 =s $

2. D将碎片 发给参与者Pi

3. D广播承诺值

4. 参与者 收到自己的碎片 后，计算下式是否成立： 如果成立，表明该碎片有效；若不成立，则请求D重发正确的碎片

3.3.2 秘密重构

重构方法同Feldman的方案。

4. 等长多项式承诺（Kate）

《Constant-Size Commitments to Polynomials and Their Applications》文献阅读笔记

4.1 介绍

对多项式承诺的两种方式：

1. 对整个多项式进行承诺

   即将这个多项式的系数通过某种方式链接在一起后进行承诺

   但在揭示多项式中的某个点的值时会同时揭示整个多项式

2. 对多项式的系数进行承诺

   即对多项式的每个系数分别进行承诺

   可以在不揭示整个多项式的情况下验证多项式在某个点的值是否与承诺一致，缺点是承诺的大小变大了。

4.2 定义

4.2.1 参数介绍

$$：安全参数

：双线性配对群，其素数阶

4.2.2 多项式承诺

1. Setup()：生成公钥PK用于承诺，其中包含合适的代数结构e
2. Commit()：使用PK对多项式进行承诺，输出承诺C和额外的信息d
3. Open()
4. VerifyPoly()
5. CreateWitness()：是在i出的证据，输出
6. VerifyEval()：验证证据

4.3 PolyCommit_DL

计算安全

前提：在 上， 总能被 整除。

1. Setup()

   和$_T g$

   为私钥，公钥为：

2. Commit()

   给定t次或小于t次的多项式，承诺。

   由于，则承诺

3. Open()

4. VerifyPoly()：验证

5. CreateWitness()：令，，输出

6. VerifyEval()：：验证 是C所承诺的多项式在下标i处的值。

4.4 PolyCommit_Ped

无条件安全

PolyCommit_DL是同态的，有多项式和，及其各自对应的承诺和。若，则，witness是

1. Setup()

   和$_T g,h$

   为私钥，公钥为：

2. Commit()

   给定t次或小于t次的多项式，选择任意t次的随机多项式，承诺。

   由于，则承诺

3. Open()

4. VerifyPoly()：验证

5. CreateWitness()：令，，输出

6. VerifyEval()：：验证 是C所承诺的多项式在下标i处的值。

4.5 eVSS

在eVSS方案的Sh和Rec阶段，VSS方法与Feldman VSS方法完全相同，只是Feldman的t + 1个形如承诺被单个多项式承诺取代。

此外，除了共享si外，秘密发放者现在还向节点Pi发送一个见证wi。

总的来说，eVSS协议需要O(1)广播，而Feldman VSS需要O(n)广播。在多次指控的情况下，秘密发放者秘密发放者可以使用§3.4中描述的批量开启功能，为整个批次提供一个证人。此外，由于PolyCommit的同态性，eVSS方案可以很容易地转换为分布式密钥生成协议。

4.5.1 秘密分发

1. D选择一个次数为t的多项式，令，并广播承诺C=Commit()
2. 对于，D计算秘密碎片 ，并CreateWitness()，输出通过安全可靠信道发送给Pi。
3. 参与者Pi收到后，运行VerifyEval()。如果验证失败则向D发送验证失败的消息。
4. D如果收到收到大于t个VerifyEval验证失败的消息，则表明这个参与者中有过多的不诚实用户，是不合格的，无法继续进行。如果少于t个，则向报告失败的用户重发==（？）==
5. 如果==revealed shares（？）== 在VerifyEval验证中失败，表明分发者D是不合格的。如果没有，表明各个参与者都接受了。

4.5.2 秘密重构

任何t + 1或更多的节点Pi发布他们接受的秘密碎片和见证。

所有t + 1(或更多)节点使用VerifyEval验证每个广播共享，然后插值对，确定秘密。

5. 高阈值异步可验证秘密共享（HAVSS）

《High-Threshold AVSS with Optimal Communication Complexity》文献阅读笔记

5.1 介绍

5.2 定义

5.2.1 算法定义

• Setup
• Com：对要求次数，并输出一个承诺字符串
• Eval：它输出一个包含i、计算值φ(i)和见证字符串wi的3元组。
• Verify：输入y是Eval输出的一个三元组，进行验证
• Hom：由于承诺的同态性质，输出的是

5.3 Haven的HAVSS协议，对一致采样的短秘密s

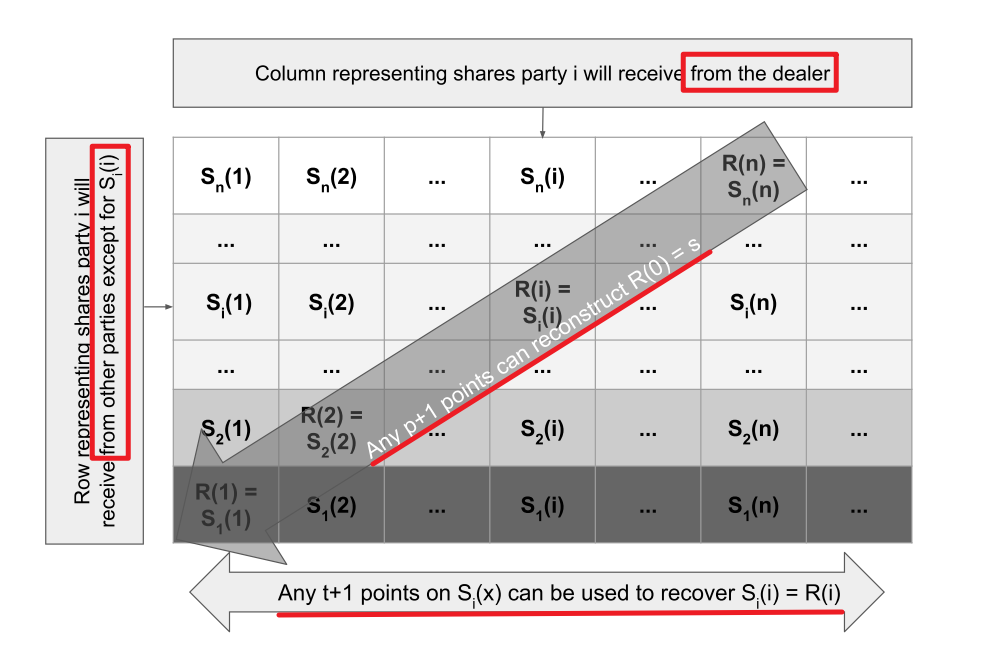
5.3.1 sharing phase

1）对秘密分发者D，收到 (ID.d, in, share, s)

1. 随机生成多项式和承诺：

   生成恢复多项式 R，次数为p，满足。

   生成n个不同的随机的共享多项式S1, S2, ..., Sn，每个参与方都会收到其中要给，次数为t，满足。

2. 计算R和Si多项式承诺：

   。这些承诺用于检验多项式的一致性。

   令。

3. 构建验证所需数据：分发者生成检验需要的数据：

   • 向量 ，其中包含第n个共享多项式 Si 在某个点的评估。这个向量中的值以转置的顺序排列，即第一个值是 S1(i)，第二个值是 S2(i)，以此类推。
   • n 个测试多项式 Ti，每个测试多项式是 R - Si，以证明份额多项式和恢复多项式之间的一致性，并计算

4. 构建根承诺：

   分发者构建了一个根承诺 ，这是一个向量承诺，包含了所有多项式承诺的信息。在后续的可靠广播协议中，服务器只会相信与根承诺 C 相关联的多项式承诺。并讲每个多项式的见证witness加入C中。

5. 发送消息给参与方：

   分发者向每个参与者发送：根承诺、恢复多项式的承诺、每个共享多项式的承诺$ _i^ST$。发送格式为：(ID.d, send, set_i)

2) 对参与者Pi，第一次从D收到消息 (ID.d, send, set_i) 时，进行回应

1. 检验： 和
2. 检验：恢复多项式的承诺和每个共享多项式的承诺都在跟承诺C中正确的位置上
3. 检验：
4. 向 发送：(ID.d, echo, info_ij) ，其中info中包含
5. 重复上述操作，

3) 对参与者Pj从Pi第一次收到消息 (ID.d, echo, info_ij) 时

1. 检验： 在C中的i位上，并且检验
2. 如果自己还没有发送ready信息，并且已经收到了 2t+1 个有效的echo信息时：向所有人发送一个ready信息 (ID.d, ready, C)

4) 对参与者Pm第一次收到消息 (ID.d, ready, C)

1. 如果自己还没有发送ready信息，等到收到 t+1 个他人发送来的ready信息后发送ready信息
2. 如果已经收到了 2t+1 个ready信息了，则等到收到 t+1 个echo 信息时：
   • 从 t+1 个有效的echo信息中对插值获得
   • 计算
   • 输出反馈信息：(ID.d, out, shared)

5.3.2 Reconstruction phase

1）receive (ID.d, in reconstruct)

向每个参与者Pj发送：(ID.d, reconstruct-share, , )

2) receive (ID.d, reconstruct-share, , )

1. 如果 在C中并且验证：

2. 如果接收到 p+1个有效的reconstruct-share 信息

   则 利用 重构出R不等式，并输入 为秘密

6. 打包异步可验证秘密共享(PAVSS)

《Bingo: Adaptively Secure Packed Asynchronous Verifiable Secret Sharing and Asynchronous Distributed Key Generation》文献阅读

6.1 Introduction

Bingo结合了所有这些增强功能：具体来说，它是一种自适应安全的打包异步可验证秘密共享(PAVSS)协议，该协议允许秘密发放者以个字的总通信复杂度共享f+1个秘密，其中n为各方的总数，f为恶意方的总数。此外，Bingo在假设n = 3f + 1时具有最佳弹性。